Search
Citation
| Huang, Y. Y., and H. J. Wang, 2020: A possible approach for decadal prediction of the PDO. J. Meteor. Res., 34(1), 63–72, doi: 10.1007/s13351-020-9144-4.. |
Article Metrics
Article views: 1013
PDF downloads: 101
Cited by: 3
With great socioeconomic and environmental significance, decadal/near-term climate prediction covering the period up to 30 yr has attracted lots of attention recently, especially for the policy-and-decision makers (Meehl et al., 2009). It has been addressed as a major issue in the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. The Decadal Climate Prediction Project (Boer et al., 2016) has been found to make contribution to the sixth Coupled Model Intercomparison Project (Eyring et al., 2016) and the World Climate Research Program (WCRP) Grand Challenge on Near Term Climate Prediction.
Pacific Decadal Oscillation (PDO), which is one of the dominant internal variability in the climate system, shows great influence on the other components of the climate system (Newman et al., 2016). For instance, its regime shifts have been suggested to contribute to the decadal climate variation over East and South Asia (Yu et al., 2015; Zhu et al., 2015; Fan and Fan, 2017), Australia (Arblaster et al., 2002) and North America (McCabe et al., 2004, 2012), and to the recent global-warming hiatus (Kosaka et al., 2013). Besides, the agriculture, water resources, and the fisheries can also be affected by the PDO (Mantua et al., 1997; Miller et al., 2004).
To predict the internal decadal climate variability is necessary but full of challenges. Currently, using initialized climate models to produce decadal climate prediction is the main technical approach. Successful strategy for initialization of the model is one of the biggest technical challenges affecting the quality of decadal climate prediction (Meehl et al., 2014; Zhou and Wu, 2017; Mehta et al., 2019). The initial shock is a long-standing problem in the model initialization (Meehl et al., 2014; He et al., 2017). In a case study, Mochizuki et al. (2010, 2012) show that the initialization in their climate model can improve the predictive skills for the PDO to some extent. Generally, the initialization shows higher improved predictive skill ability in North Atlantic (e.g., Smith et al., 2010; Yang et al., 2013) than in North Pacific (Guemas et al., 2012; Kim et al., 2012; Newman, 2013; Meehl and Teng, 2014; Wang and Miao, 2018), because of the inherent sensitivity to initial state uncertainty (Branstator et al., 2012; Branstator and Teng, 2012) and the uncertainty in the mechanism for internally generated decadal climate variability in the Pacific (Meehl et al., 2014). Moreover, the regime shift prediction for the PDO is sometimes considered to be challengeable because it may be largely and randomly forced (Newman et al., 2016). Some statistical/statistical–dynamical method are used to predict the surface air temperature in the following decades (e.g., Fu et al., 2011, Luo and Li, 2014), but none of them for the PDO. Therefore, the current decadal prediction of PDO is far from being successful.
It is worth noticing that the recent interannual increment approach seems to provide a new clue in the climate prediction (Wang et al., 2012). The predictand is the interannual increment of a variable (difference between the current year and the preceding year) instead of the traditional variable anomalies from the climatology. The final predicted variable is produced by adding the predicted interannual increment to the observed variable in the preceding year. Since the preceding observed variable contains decadal–interdecadal signals (Wang et al., 2010) and the interannual increment of the variable in the numerical climate model can reduce the model system bias (Huang et al., 2014), the interannual increment approach has made some achievements in the interan-nual climate prediction (e.g. Fan et al., 2008; Fan, 2009, 2010; Fan and Wang, 2009; Tian and Fan, 2015).
In the traditional decadal prediction steps, the predictand in each following year is usually predicted firstly, and then the decadal variability is obtained through the filter or running mean. In this study, we will directly use the decadal variability of the PDO as the predictand. The increment approach is used to build the statistical model to improve the effective samples and obtain more information from the previous observation. Section 2 gives the data and method in details. Sections 3 and 4 show the prediction of the decadal variability for the PDO index and the SSTA over North Pacific, respectively. A summary is presented in Section 5.
In this paper, we focus on the decadal prediction of the PDO during winter season (December–January–February, DJF), because many of the physical processes in the North Pacific have undergone a substantial long-term intensification during winter (Mantua et al., 1997; Deser and Phillips, 2006; Yeh et al., 2011; Wang et al., 2012). Five-year running mean is used to obtain the decadal vari-ability, and the yearly mark represents the middle year of the 5-yr mean period. The decadal PDO index is defined as the leading principal component of the empirical orthogonal function of 5-yr running mean DJF SSTAs over the North Pacific (20°–70°N), in which the SSTAs are the anomalies from the climatological annual cycle after removing the global mean SSTs (Mantua et al., 1997).
Four types of monthly mean datasets are involved to predict the decadal PDO, including: sea surface temperature from NOAA Extended Reconstructed SST v3b on a horizontal resolution of 2° x 2° (Smith et al., 2008), sea surface height from SODA (Simple Ocean Data Assimilation) v2.1.6 on a horizontal resolution of 0.5° x 0.5° (Carton and Giese, 2008), sea level pressure from NOAA-CIRES (Cooperative Institute for Research in Environmental Sciences) 20th Century Reanalysis version 2c on a horizontal resolution of 2° x 2° (Compo et al., 2011), and sea ice concentration on a horizontal resolution of 1° x 1° from the Met Office Hadley Centre (Rayner et al., 2003).
After obtaining the decadal PDO index, the difference of the PDO between the current year and the three years before is calculated as the 3-yr decadal increment (DI) of the PDO (namely DI_PDO) [see Eq. (1)]. For example, the DI_PDO in 1906 is the difference between PDO in 1906 and PDO in 1903.
| DI_PDOi=PDOi−PDOi−3, | (1) |
where PDOi and PDOi−3 represent the decadal PDO index in current year and three years before the current year, respectively. DI_PDOi indicates the decadal increment of the PDO in current year.
The DI_PDO is predicted firstly through a statistical model with three predictors, which are also in the DI form (DI_Predictors). DI_Predictors are calculated as the 3-yr decadal increment of the 5-yr running mean for the detrended seasonal mean predictors. The final predicted PDO is derived by adding the predicted DI_PDO to the observed PDO three years ago by using Eq. (2) below,
| PDOi=PDOobsi−3+DI_PDOs-modeli, | (2) |
where
In order to avoid the artificial built-in skill, we use two modulated validation methods to verify the predictive skill of the statistical model. (1) Cross-validation with five years left out (Michaelsen, 1987): the predictand in a target year is predicted with the forecast model by using the training samples in all the years except the five years that are centered around the target year. This process is repeated for all the other target years to obtain the cross-validated re-forecast for the whole prediction period. The first/last three years are predicted by leaving the first/last five years out from the prediction period. (2) Independent hindcast: the training period is the forward-rolling 67 yr, which is from 72 (69) yr before the target year to 6 (3) yr before the target year in predictors (predictand) to avoid the prediction model using any information from the prediction period. For example, the DI_PDO in 1975 (1976) is predicted by the DI_Predictors in 1972 (1973) based upon the forecast model built up using the period of 1903–1969/1906–1972 (1904–1970/1907–1973) in DI_Predictors/DI_PDO.
The moving t test (MTT) with a 9-yr moving window is used to detect the abrupt change points of the decadal variation of the PDO. The student’s t-test is used to examine the statistical significance, in which the effective sample size N* is computed following Bretherton et al. (1999) and Ding et al. (2012) as follows,
| N∗=N1−r1r21+r1r2, |
where N is the number of available time steps, and r1 and r2 are the lag-1 autocorrelation of the two correlated variables, respectively.
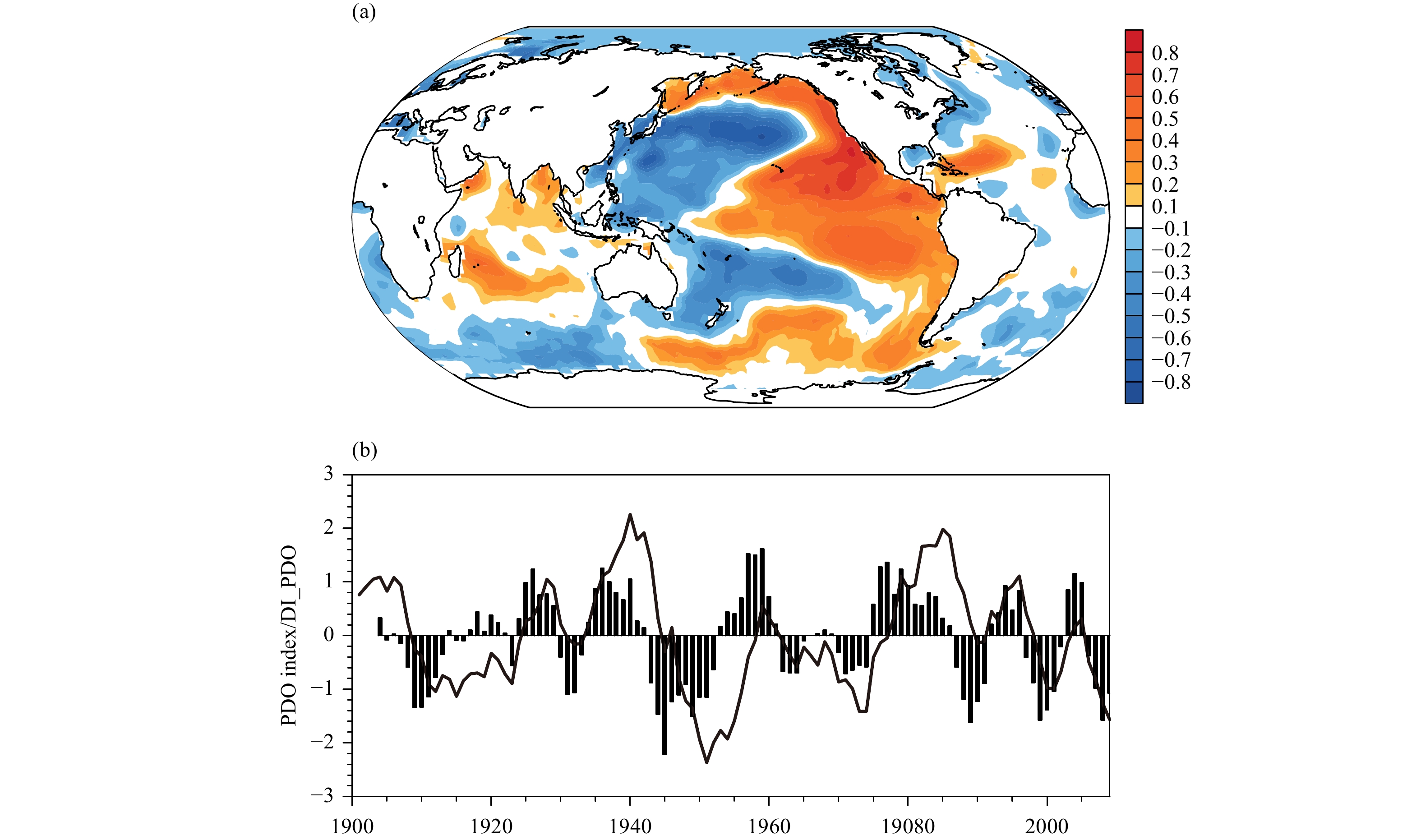
Figure 1a shows the spatial patterns of the decadal DJF global SST associated with the decadal PDO index (the first EOF of decadal DJF SSTAs over the North Pacific). This mode accounts for 27% of North Pacific decadal SST variance. A positive PDO features negative SSTAs over central and western North Pacific and positive SSTAs over eastern North Pacific and eastern tropi-cal Pacific. The decadal DJF PDO index during 1901–2009, as well as the DI_PDO, is shown in Fig. 1b.
The DI_PDO is treated as the predictand. The empiri-cal statistical model is built to predict the DI_PDO using DI_Predictors. This empirical statistical model is built through three steps. First, the potential preceding DI_Predictors are derived from the following three main processes driving the PDO as summarized by Newman et al. (2016): a) fluctuations in the Aleutian low; b) teleconnections from the tropics; and c) midlatitude ocean dynamics and coupled variability. Second, the DI_Predictors have to lead the DI_PDO at least three years to avoid the DI_Predictors using any information from the prediction period, since we use 5-yr running mean to derive the decadal variability. Third, we use stepwise regression to identify the final DI_Predictors, which should be important and less dependent, to build the empirical statistical model. The fundamental rules in the stepwise regression are to select the DI_Predictor that is most significantly correlated to the predictand, and remove those predictors that are significantly related to this DI_Predictor, thus the DI_Predictors selected this way are independent to each other. We use the 99% confidence level for Fisher’s F test to select the final DI_Predictors.
Based on the above steps, three leading DI_Predictors for three years are selected, which are autumn DI of Aleutian low (DI_AL), winter DI of sea ice over of Greenland Sea (DI_SIC), and spring DI of sea surface height over central Pacific (DI_SSH), respectively [Eq. (4)]. Physically, the SST variability over most of the North Pacific is driven primarily by the atmospheric forcing (Smirnov et al., 2014). Generally, the atmospheric variations lead the SST variations that are resulted from the physical processes of the flux-driven SSTA pattern or Ekman transports (Davis, 1976; Deser and Timlin, 1997). The preceding Aleutian low (AL) has been suggested to be one of the important atmospheric forcing to drive the PDO variability (Schneider and Cornuelle, 2005; Newman et al., 2016) (Fig. 2a). On the other hand, the SIC anomalies over Greenland Sea is connected to the PDO variability through influencing the Arctic Oscillation anomalies (Fig. 2b) (Lindsay and Zhang, 2005; Sun and Wang, 2006). Additionally, the sub-Arctic frontal zone (SAFZ) over the western Pacific has the large SST variations associated with the PDO (Nakamura and Kazmin, 2003). The preceding thermal capacity over SAFZ can drive the PDO variability through thermodynamic response (Fig. 2c) (Qiu, 2003; Newman et al., 2016).
| DI_PDO=−0.31×DI_AL−0.36×DI_SIC−0.37×DI_SSH, | (3) |
where DI_AL represents DI of the September–October–November sea level pressure averaged over 36°–44°N, 180°–166°W; DI_SIC indicates DI of the DJF sea ice concentration averaged over Greenland Sea (70°–75°N, 15°–2°W); and DI_SSH is the DI of March–April–May sea surface height averaged over central Pacific (28°–33°N, 155°–140°W). The DI_AL, DI_SIC, and DI_SSH explain 9.6%, 13%, and 13.7% of the DI_PDO variance, respectively.
The correlation coefficients of the DI_PDO during 1906–2009 with DI_AL, DI_SSH, and DI_SIC during 1903–2006 are −0.43, −0.48, and −0.43, respectively. Although three of the DI_Predictors are all significantly correlated with DI_PDO, it is inevitable that these relationships have decadal shifts since the predicted period is more than 100 years (Fig. 3). It is noted that both of the relationships in DI_AL and DI_SSH become weakened around the period of 1960–1980, which may influence the predictive effect in the statistical model during this period (Figs. 3a, b). The moderate explained variances from the three DI_Predictors for the DI_PDO may also hint this decadal shift in the correlations.
Figure 4a shows the predicted DI_PDO during 1906–2009 in the cross-validation with 5 years left out. As we can see, the limited skill for the predicted DI_PDO appears over the period around 1960–1980, which may be attributed to the above mentioned weakened relationships in DI_AL and DI_SSH. Excluding the period of 1960–1980, the predicted DI_PDO shows consistency in variability and amplitude with the observed DI_PDO to some extent, especially for the period after 1980. The correlation coefficient (CC) between the observed and predicted DI_PDO is 0.68 during 1906–2009 (significant at the 99.9% confidence level). The statistical model in general displays a reasonable predictive skill for the DI_PDO.
The predicted DI_PDO is added with the PDO three years ago in the observation to obtain the final predicted PDO (Fig. 4c). The inconsistency between the predicted and observed PDO during 1960–1980 can also be seen in Fig. 4c. In the rest of the prediction period, the final predicted PDO fits the observation very well in amplitude and variability and generally successfully captures the phase change at each time. The CC between the observed and final predicted PDO reaches 0.82 during 1906–2009 (Fig. 4c). Actually, compared to regime shifts in the observation, the errors for each regime shift in prediction is less than or equal to two years (Fig. 4e). Overall, the increment method employed in this study shows effective skill for the decadal prediction of the PDO.
The predictive skill of the statistical model is further investigated by examining the independent hindcast for predicting the DI_PDO during 1975–2009. The magnitude of the predicted DI_PDO during 1975–1980 is lower than 0.5, which is far less than the observation, indicating a limited predictive skill. After 1980, the statistical model displays a high predictive skill for the DI_PDO. The CC between the prediction and observation of the DI_PDO during 1975–2009 can reach 0.78 (significant at the 99% confidence level) (Fig. 4b). The final predicted PDO during 1975–2009 has the CC of 0.81 with the observation (Fig. 4d). There are two regime shifts in observed PDO during 1975–2009, which are 1988/1989 and 1999/2000, respectively. The final predicted PDO has the first regime shift at 1990/1991, which is two years later than the observation. The second regime shift in the final predicted PDO is at 1999/2000, which is precisely consistent with the observation (Fig. 4f). Overall, the statistical model combined with the increment method presents a high skill for the decadal prediction of the PDO, including the prediction for the regime shift.
In order to identify the effect of the increment method, the statistical prediction model in its original form (i.e., without the increment method) is used to directly predict PDO [Eq. (5)]. According to the correlation map of the PDO and the 3-yr leading predictors (Fig. 5), the key areas for the AL and SSH move slightly to the highest correlation regions compared to the key areas for DI_AL and DI_SSH. The key areas for the SIC move to the north of Kara Sea, since the region in Greenland Sea is not significant any more.
| PDO=−0.36×AL−0.35×SIC−0.37×SSH, | (4) |
where AL indicates the September–October–November (SON) sea level pressure over 35°–50°N, 175°E–160°W; SIC represents DJF sea ice concentration over 78°–85°N, 70°–90°E; SSH is the sea surface height over 30°–35°N, 170°–145°W. AL, SIC, and SSH explain, respectively, 13%, 12.3%, and 13.7% of the PDO variance.
The CCs of the PDO during 1906–2009 with 3-yr leading AL, SSH, and SIC are −0.48, −0.55, and −0.56, respectively, which are all above the 90% confidence level. The statistical model in its original form seems to show certain skill in predicting the PDO with significant correlation coefficient between the prediction and the observation (Figs. 6a, c). However, the cross-validated PDO shows that the extreme negative period of PDO index around 1950 has been missed (Fig. 6a). In the independent hindcast for the PDO during 1975–2009 (Figs. 6b, d), the magnitude of the prediction is much lower than the observation and the predicted PDO keeps in the negative phase after the late 1980s, which is incorrect according to the observation. Generally, the predictive skill of the statistical predictive model without the increment method is lower than that with the increment method.
The statistical predictive model combined with the increment method is also employed to predict the decadal variability of the DJF SSTA at each grid point over the North Pacific Ocean (20°–70°N). Equation (6) is the same as Eq. (4), except that the predictand is the DI of DJF SSTA (DI_SSTA) over the North Pacific. The DI_Predictors also lead the DI_SSTA variability by three years. The final predicted SSTA is obtained by adding the predicted DI_SSTA to the observed SSTA three years ago. The predictive skill is tested by the independent hindcast for the DI_SSTA during 1975–2009.
| DI−SSTA=a×DI−AL+b×DI−SIC+c×DI−SSH. | (5) |
For the DI_SSTA during 1975–2009, a significantly high predictive skill appears over the Kuroshio–Oyashio Extensions to the central Pacific and the region north of 50°N (Fig. 7a). Although the predictive skill for the final predicted SSTA is not impeccable (Fig. 7b), the final predicted SSTA successfully demonstrates a regime shift at 1999 (Fig. 7c), which is a challenge for current dynamic numerical models (Newman et al., 2016). Moreover, we further investigate the predictive skill of this statistical model combined with the increment method to produce the spatial pattern of the PDO. Figure 7d gives the CC between the final predicted PDO index (Fig. 4d) and the final predicted SSTA over the North Pacific (Fig. 7b) in the independent hindcast. Corresponding to the positive PDO, there are negative SSTAs appearing over the western and central North Pacific and positive SSTAs appearing over the eastern North Pacific, resembling the observation (Fig. 7e). Actually, the pattern correlation coefficients between predictions and observations reaches 0.95. The statistical model combined with the increment method shows a high predictive skill for the regime shift of the SSTA over North Pacific and the spatial pattern of the PDO.
In this study, the decadal variability of the PDO is predicted by a statistical model combined with the increment method. Particularly, all the involved data have been detrended and applied with a 5-yr running meaning to maximize the decadal variability. The 3-yr increment of the PDO (DI_PDO) is predicted firstly by the statisti-cal model with DI_AL, DI_SSH, and DI_SIC at preceding three years. The predicted DI_PDO is then added with the PDO three years ago in the observation to derive the final predicted PDO. The statistical model combined with the increment method shows a high predictive skill for the decadal variability of the PDO, especially for its regime shifts.
In addition to the fact that the increment method can take advantage of the previous observation, another benefit is that the increment method can increase the effective sample size after we apply the 5-yr running mean to the meta data. For example, for the correlation between DJF PDO during 1906–2009 and DJF SIC over Greenland Sea during 1903–2006, the effective sample size is 8, but it is 19 in correlation between DI_PDO and DI_SIC. The increment method provides a possibility for directly focusing on the decadal variability prediction of the PDO.
Our results provide a promising clue in current de-cadal climate prediction, especially for the regime shift prediction. This new method can be applied for decadal climate prediction on other modes (e.g., Atlantic multidecadal oscillation) and predictands (e.g., sea surface temperature). Additionally, the increment method may be applicable to the current decadal prediction products of climate models. The DI of the variable may be more predictable in the numerical model than the original form of the variable, since the DI form can partly reduce the system bias in the climate model. We can add the DI form prediction in climate models to the observed value at previous year to improve the model’s prediction. Also, we can build a dynamical–statistical model using the DI form prediction in climate models and previous observations, to provide more realistic decadal climate prediction.
Fig. 2. Correlation coefficients of the DJF DI-PDO during 1906–2009 with 3-yr leading (a) SON DI of sea level pressure, (b) MAM DI of sea surface height, and (c) DJF DI of sea ice concentration. The area with dots indicate values significant at the 90% confidence level with the student t-test. The boxes indicate the key areas for calculating the DI_Predictors, including DI_AL (36°–44°N, 180°–166°W), DI_SSH (28°–33°N, 155°–140°W), and DI_SIC (70°–75°N, 15°–2°W).
Fig. 3. The 25-yr running correlation of the DI_PDO during 1906–2009 with (a) DI_AL, (b) DI_SSH, and (c) DI_SIC in preceding three years. The thin dashed line denotes the 90% confidence level. The effective sample sizes are the maximum value in the slipping 25 yr, which are 13, 13, and 10 for DI_AL, DI_SSH, and DI_SIC, respectively.
Fig. 4. Prediction of the DJF DI_PDO, PDO, and the regime shifts of the PDO detected by moving t test with 9-yr moving window in cross-validation with five years left out for the period of 1906–2009 (left panels) and in independent hindcast for the period of 1975–2009 (right panels). The thick black (red) line with hollow circles (rhombus) represents the result of observation (prediction). The pink shading is the 95% prediction interval. The numbers in the upper right corner is the temporal correlation coefficient between the prediction and observation. The thin black solid lines in panels (e) and (f) indicate the values significant at the 95% and 99% confidence level, respectively.
Fig. 5. Correlation coefficients of DJF PDO during 1906–2009 with 3-yr leading (a) SON sea level pressure, (b) MAM sea surface height, and (c) DJF sea ice concentration. The area with dots indicate the values significant above the 90% confidence level. The boxes are the key areas for calculating predictors, which are AL (35°–50°N, 175°E–160°W), SSH (30°–35°N, 170°–155°W), and SIC (78°–85°N, 70°–90°E), respectively.
Fig. 6. As in Fig. 4, but for the PDO prediction of the statistical model with 3-yr leading AL, SSH, and SIC. (a, c) are the cross-validated PDO during 1906–2009 and its 9-yr MTT results; (b, d) are the predicted PDO during 1975–2009 in the independent hindcast and its 9-yr MTT results.
Fig. 7. Correlation coefficients of the observation with (a) the predicted DJF DI_SSTA and (b) the final predicted DJF SSTA in the independent hindcast during 1975–2009. (c) Difference of the predicted DJF SSTA in the independent hindcast between 2000–2009 and 1980–1999. (d, e) Correlation coefficient of the PDO index with the SSTA over North Pacific in independent hindcast and observation, respectively. The area with dots indicate the values significant above the 90% (panels a, b) or 95% (panel c) confidence level using the Student’s t-test.
|
Arblaster, J., G. Meehl, and A. Moore, 2002: Interdecadal modulation of Australian rainfall. Climate Dyn., 18, 519–531. doi: 10.1007/s00382-001-0191-y
|
|
Boer, G. J., D. M. Smith, C. Cassou, et al., 2016: The Decadal Climate Prediction Project (DCPP) contribution to CMIP6. Geosci. Model Dev., 9, 3751–3777. doi: 10.5194/gmd-9-3751-2016
|
|
Branstator, G., and H. Teng, 2012: Potential impact of initialization on decadal predictions as assessed for CMIP5 models. Geophy. Res. Lett., 39, L12703. doi: 10.1029/2012GL051974
|
|
Branstator, G., H. Teng, G. A. Meehl, et al., 2012: Systematic estimates of initial-value decadal predictability for six AOGCMs. J. Climate, 26, 1827–1846. doi: 10.1175/JCLI-D-11-00227.1
|
|
Bretherton, C. S., M. Widmann, V. P. Dymnikov, et al., 1999: The effective number of spatial degrees of freedom of a time-varying field. J. Climate, 12, 1990–2009. doi: 10.1175/1520-0442(1999)012<1990:TENOSD>2.0.CO;2
|
|
Carton, J. A., and B. S. Giese, 2008: A reanalysis of ocean climate using Simple Ocean Data Assimilation (SODA). Mon. Wea. Rev., 136, 2999–3017. doi: 10.1175/2007mwr1978.1
|
|
Compo, G. P., J. S. Whitaker, P. D. Sardeshmukh, et al., 2011: The twentieth century reanalysis project. Quart. J. Roy. Meteor. Soc., 137, 1–28. doi: 10.1002/qj.776
|
|
Davis, R. E., 1976: Predictability of sea surface temperature and sea level pressure anomalies over the North Pacific Ocean. J. Phys. Oceanogr., 6, 249–266. doi: 10.1175/1520-0485(1976)006<0249:POSSTA>2.0.CO;2
|
|
Deser, C., and M. S. Timlin, 1997: Atmosphere–ocean interaction on weekly timescales in the North Atlantic and Pacific. J. Climate, 10, 393–408. doi: 10.1175/1520-0442(1997)010<0393:AOIOWT>2.0.CO;2
|
|
Deser, C., and A. S. Phillips, 2006: Simulation of the 1976/77 climate transition over the North Pacific: Sensitivity to tropical forcing. J. Climate, 19, 6170–6180. doi: 10.1175/JCLI3963.1
|
|
Ding, Q. H., E. J. Steig, and D. S. Battisti, et al., 2012: Influence of the tropics on the southern annular mode. J. Climate, 25, 6330–6348. doi: 10.1175/JCLI-D-11-00523.1
|
|
Eyring, V., S. Bony, G. A. Meehl, et al., 2016: Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev., 9, 1937–1958. doi: 10.5194/gmd-9-1937-2016
|
|
Fan, K., 2009: Predicting winter surface air temperature in Northeast China. Atmos. Ocean. Sci. Lett., 2, 14–17. doi: 10.1080/16742834.2009.11446770
|
|
Fan, K., 2010: A prediction model for Atlantic named storm frequency using a year-by-year increment approach. Wea. Forecasting, 25, 1842–1851. doi: 10.1175/2010WAF2222406.1
|
|
Fan, K., and H. J. Wang, 2009: A new approach to forecasting typhoon frequency over the western North Pacific. Wea. Forecasting, 24, 974–986. doi: 10.1175/2009WAF2222194.1
|
|
Fan, K., H. J. Wang, and Y. J. Choi, 2008: A physically-based statistical forecast model for the middle–lower reaches of the Yangtze River Valley summer rainfall. Chinese Sci. Bull., 53, 602–609. doi: 10.1007/s11434-008-0083-1
|
|
Fan, Y., and K. Fan, 2017: Pacific Decadal Oscillation and the decadal change in the intensity of the interannual variability of the South China Sea summer monsoon. Atmos. Ocean. Sci. Lett., 10, 162–167. doi: 10.1080/16742834.2016.1256189
|
|
Fu, C. B., C. Qian, and Z. H. Wu, 2011: Projection of global mean surface air temperature changes in next 40 years: Uncertainties of climate models and an alternative approach. Sci. China Earth Sci., 54, 1400–1406. doi: 10.1007/s11430-011-4235-9
|
|
Guemas, V., F. J. Doblas-Reyes, F. Lienert, et al., 2012: Identifying the causes of the poor decadal climate prediction skill over the North Pacific. J. Geophys. Res. Atmos., 117, D20111. doi: 10.1029/2012JD018004
|
|
He, Y. J., B. Wang, M. M. Liu, et al., 2017: Reduction of initial shock in decadal predictions using a new initialization strategy. Geophys. Res. Lett., 44, 8538–8547. doi: 10.1002/2017gl074028
|
|
Huang, Y. Y., H. J. Wang, and K. Fan, 2014: Improving the prediction of the summer Asian–Pacific Oscillation using the interannual increment approach. J. Climate, 27, 8126–8134. doi: 10.1175/JCLI-D-14-00209.1
|
|
Kim, H.-M., P. J. Webster, and J. A. Curry, 2012: Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys. Res. Lett., 39, L10701. doi: 10.1029/2012GL051644
|
|
Kosaka, Y., and S. P. Xie, 2013: Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature, 501, 403–407. doi: 10.1038/nature12534
|
|
Lindsay, R. W., and J. Zhang, 2005: The thinning of Arctic sea ice, 1988–2003: Have we passed a tipping point? J. Climate, 18, 4879–4894. doi: 10.1175/JCLI3587.1
|
|
Luo, F. F., and S. L. Li, 2014: Joint statistical–dynamical approach to decadal prediction of East Asian surface air temperature. Sci. China Earth Sci., 57, 3062–3072. doi: 10.1007/s11430-014-4984-3
|
|
Mantua, N. J., S. R. Hare, Y. Zhang, et al., 1997: A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Amer. Meteor. Soc., 78, 1069–1079. doi: 10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2
|
|
McCabe, G. J., M. A. Palecki, and J. L. Betancourt, 2004: Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proc. Natl. Acad. Sci. USA, 101, 4136–4141. doi: 10.1073/pnas.0306738101
|
|
McCabe, G. J., T. R. Ault, B. I. Cook, et al., 2012: Influences of the El Niño Southern Oscillation and the Pacific Decadal Oscillation on the timing of the North American spring. Int. J. Climatol., 32, 2301–2310. doi: 10.1002/joc.3400
|
|
Meehl, G. A., and H. Y. Teng, 2014: CMIP5 multi-model hindcasts for the mid-1970s shift and early 2000s hiatus and predictions for 2016–2035. Geophys. Res. Lett., 41, 1711–1716. doi: 10.1002/2014GL059256
|
|
Meehl, G. A., L. Goddard, J. Murphy, et al., 2009: Decadal prediction: Can it be skillful? Bull. Amer. Meteor. Soc., 90, 1467–1486. doi: 10.1175/2009BAMS2778.1
|
|
Meehl, G. A., L. Goddard, G. Boer, et al., 2014: Decadal climate prediction: An update from the trenches. Bull. Amer. Meteor. Soc., 95, 243–267. doi: 10.1175/BAMS-D-12-00241.1
|
|
Mehta, V. M., K. Mendoza, and H. Wang, 2019: Predictability of phases and magnitudes of natural decadal climate variability phenomena in CMIP5 experiments with the UKMO HadCM3, GFDL-CM2.1, NCAR-CCSM4, and MIROC5 global earth system models. Climate Dyn., 52, 3255–3275. doi: 10.1007/s00382-018-4321-1
|
|
Michaelsen, J., 1987: Cross-validation in statistical climate forecast models. J. Appl. Meteor., 26, 1589–1600. doi: 10.1175/1520-0450(1987)026<1589:CVISCF>2.0.CO;2
|
|
Miller, A. J., F. Chai, S. Chiba, et al., 2004: Decadal-scale climate and ecosystem interactions in the North Pacific Ocean. J. Oceanogr., 60, 163–188. doi: 10.1023/b:joce.0000038325.36306.95
|
|
Mochizuki, T., M. Ishii, M. Kimoto, et al., 2010: Pacific Decadal Oscillation hindcasts relevant to near-term climate prediction. Proc. Natl. Acad. Sci. USA, 107, 1833–1837. doi: 10.1073/pnas.0906531107
|
|
Mochizuki, T., Y. Chikamoto, M. Kimoto, et al., 2012: Decadal prediction using a recent series of MIROC global climate models. J. Meteor. Soc. Japan, 90A, 373–383. doi: 10.2151/jmsj.2012-A22
|
|
Nakamura, H., and A. S. Kazmin, 2003: Decadal changes in the North Pacific oceanic frontal zones as revealed in ship and satellite observations. J. Geophys. Res. Oceans, 108, 3078. doi: 10.1029/1999JC000085
|
|
Newman, M., 2013: An empirical benchmark for decadal forecasts of global surface temperature anomalies. J. Climate, 26, 5260–5269. doi: 10.1175/jcli-d-12-00590.1
|
|
Newman, M., M. A. Alexander, T. R. Ault, et al., 2016: The Pacific decadal oscillation, revisited. J. Climate, 29, 4399–4427. doi: 10.1175/JCLI-D-15-0508.1
|
|
Qiu, B., 2003: Kuroshio Extension variability and forcing of the Pacific Decadal Oscillations: Responses and potential feedback. J. Phys. Oceanogr., 33, 2465–2482. doi: 10.1175/2459.1
|
|
Rayner, N. A., D. E. Parker, E. B. Horton, et al., 2003: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos., 108, 4407. doi: 10.1029/2002JD002670
|
|
Schneider, N., and B. D. Cornuelle, 2005: The forcing of the Pacific Decadal Oscillation. J. Climate, 18, 4355–4373. doi: 10.1175/JCLI3527.1
|
|
Smirnov, D., M. Newman, and M. A. Alexander, 2014: Investigating the role of ocean–atmosphere coupling in the North Pacific Ocean. J. Climate, 27, 592–606. doi: 10.1175/JCLI-D-13-00123.1
|
|
Smith, D. M., R. Eade, N. J. Dunstone, et al., 2010: Skilful multi-year predictions of Atlantic hurricane frequency. Nat. Geosci., 3, 846–849. doi: 10.1038/ngeo1004
|
|
Smith, T. M., R. W. Reynolds, T. C. Peterson, et al., 2008: Improvements to NOAA’s historical merged land–ocean surface temperature analysis (1880–2006). J. Climate, 21, 2283–2296. doi: 10.1175/2007JCLI2100.1
|
|
Sun, J. Q., and H. J. Wang, 2006: Relationship between Arctic Oscillation and Pacific Decadal Oscillation on decadal timescale. Chinese Sci. Bull., 51, 75–79. doi: 10.1007/s11434-004-0221-3
|
|
Tian, B. Q., and K. Fan, 2015: A skillful prediction model for winter NAO based on Atlantic sea surface temperature and Eurasian snow cover. Wea. Forecasting, 30, 197–205. doi: 10.1175/WAF-D-14-00100.1
|
|
Wang, H. J., Y. Zhang, and X. M. Lang, 2010: On the predictand of short-term climate prediction. Climatic Environ. Res., 15, 225–228. (in Chinese) doi: 10.3878/j.issn.1006-9585.2010.03.01
|
|
Wang, H. J., K. Fan, X. M. Lang, et al., 2012: Initiating and applying the interannual increment prediction approach. Advances in Climate Prediction Theory and Technique of China, China Meteorological Press, 120–139. (in Chinese)
|
|
Wang, T., and J. P. Miao, 2018: Twentieth-century Pacific Decadal Oscillation simulated by CMIP5 coupled models. Atmos. Ocean. Sci. Lett., 11, 94–101. doi: 10.1080/16742834.2017.1381548
|
|
Wang, T., O. H. Otterå, Y. Q. Gao, et al., 2012: The response of the North Pacific decadal variability to strong tropical volca-nic eruptions. Climate Dyn., 39, 2917–2936. doi: 10.1007/s00382-012-1373-5
|
|
Yang, X. S., A. Rosati, S. Q. Zhang, et al., 2013: A predictable AMO-like pattern in the GFDL fully coupled ensemble initialization and decadal forecasting system. J. Climate, 26, 650–661. doi: 10.1175/jcli-d-12-00231.1
|
|
Yeh, S. W., Y. J. Kang, Y. Noh, et al., 2011: The North Pacific climate transitions of the winters of 1976/77 and 1988/89. J. Climate, 24, 1170–1183. doi: 10.1175/2010jcli3325.1
|
|
Yu, L., T. Furevik, O. H. Otterå, et al., 2015: Modulation of the Pacific Decadal Oscillation on the summer precipitation over East China: A comparison of observations to 600-years control run of Bergen Climate Model. Climate Dyn., 44, 475–494. doi: 10.1007/s00382-014-2141-5
|
|
Zhou, T. J., and B. Wu, 2017: Decadal climate prediction: Scienti-fic frontier and challenge. Adv. Earth Sci., 32, 331–341. (in Chinese) doi: 10.11867/j.issn.1001-8166.2017.04.0331
|
|
Zhu, Y. L., H. J. Wang, J. H. Ma, et al., 2015: Contribution of the phase transition of Pacific Decadal Oscillation to the late 1990s’ shift in East China summer rainfall. J. Geophys. Res. Atmos., 120, 8817–8827. doi: 10.1002/2015jd023545
|
| 1. | Zhixiong Yao, Dongfeng Xu, Jun Wang, et al. Predicting and Understanding the Pacific Decadal Oscillation Using Machine Learning. Remote Sensing, 2024, 16(13): 2261. DOI:10.3390/rs16132261 |
| 2. | Danwei Qian, Yanyan Huang, Huijun Wang. A preliminary attempt on decadal prediction of the East Asian summer monsoon. Theoretical and Applied Climatology, 2022, 148(3-4): 1499. DOI:10.1007/s00704-022-04011-w |
| 3. | Lifan Chen, Lijuan Cao, Zijiang Zhou, et al. A New Globally Reconstructed Sea Surface Temperature Analysis Dataset since 1900. Journal of Meteorological Research, 2021, 35(6): 911. DOI:10.1007/s13351-021-1098-7 |